How Are Perpetual Options Priced?

We'll cover:

• Tradefeed-pricing
• Orderbook-based pricing
• Black-Scholes pricing
• Proprietary pricing
• The pricing employed by Everstrike, a world-leading perpetual options exchange

Tradefeed-pricing

This is the simplest, but least accurate pricing method.

In this method, you simply price the options contract according to the last traded price. If the last trade (of an identical contract) took place at $1,500, you consider this the price of the contract.

This method can have decent accuracy if the last trade took place relatively recently. However, it fails to include any development that has taken place since the trade happened. Key factors, that were used to determine the previous price, such as the price of the underlier, the volatility estimate of the underlier and the TTNF (time till next funding) of the contract, may have changed significantly, rendering this pricing method completely inaccurate and useless.

Orderbook-based pricing

This method uses live order-book data to determine the price of the perpetual options contract.

The price could be one of the following:

• The mid price (the average of the best bid and the best ask)
• The impact price (the average fill price for two sufficiently large trades, in either direction)

While this method could be considered an improvement compared to the previous method (by incorporating live data from market participants), it suffers from two major drawbacks:

• Market participants are not always well-informed
• Market participants with sufficient capital (whales) are able to take control of the order-book and manipulate the mid price or impact price to their liking

However, the pricing method remains a useful tool in efficient markets (markets with many participants and large amounts of liquidity).

Black-Scholes pricing

This method calculates a theoretical price for the options contract, based on the widely accepted Black-Scholes formula.

The Black-Scholes formula was established decades ago by academics and uses the following properties to make a price estimate:

• Price of the underlier
• Expected future volatility of the underlier
• Time till contract expiration
• Risk-free interest rate
• Contract strike price

While not perfect, it has been used extensively throughout the past 50 years, and has generated a significant amount of recognition. It is now the most commonly accepted way of pricing European-style options, and is taught in every College finance class.

To be used with perpetual options, the formula needs to be modified slightly.

Instead of incorporating the time till contract expiration, which does not exist for perpetual options, the Funding Period needs to be used. The Funding Period can be considered a proxy for expiration, since 50% of a perpetual options contract effectively expires and is rolled over, at time of funding.

The formula that can be used with perpetual options looks like this:

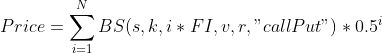
If you think this formula looks nothing like the original Black-Scholes used for European-style options, you may be correct!

However, there's not actually a lot of changes going on:

• We are substituting the contract's time till maturity (expiration) with its funding period.
• We are executing the Black-Scholes formula multiple times, multiplying each result with a multiplier, and summing the multiplied results together. The result of the summation is our final result.

Choosing a sufficiently high N is important for accuracy. A N of 10 is generally recommended. Lower N's will tend to yield inaccurate results, and higher N's may render the formula too computationally expensive, while only improving the accuracy marginally.

A N of 10 makes the formula ten times more computationally expensive than the original Black-Scholes formula. This is generally not a problem (Black-Scholes is already quite efficient and runs in milliseconds on modern hardware). The only case where it could be a problem is when you are a high-frequency options market maker and need to calculate price quotes in microseconds in order to maintain speed and competitiveness.

If you do not want to go through the hassle of executing the Black-Scholes multiple times, you can also use the original Black-Scholes to provide a rough price estimate. This can be achieved by substituting time till maturity with Funding Period * 20 in the original formula, and executing the formula as normal.

Proprietary pricing

Different market participants may have their own proprietary pricing methods for perpetual options. Some may use classic alternatives to the Black-Scholes method such as the binomial pricing model. Others may use machine learning.

However, none of these methods are public. The only public pricing method for perpetual options pricing at the time of writing this article is the modified Black-Scholes method that was presented in the section above.

If you can establish your own proprietary pricing method that is superior to the Black-Scholes, you may be able to gain an edge in the market.

Pricing used on Everstrike

Everstrike uses a combination of Black-Scholes pricing and orderbook-based pricing to determine the fair price of a perpetual options contract. The fair price is known as the Mark Price within the Everstrike platform, and is used for the purpose of liquidating positions. It is also the basis of U/PL (unrealised profit/loss) calculations within the Everstrike Frontend app.

If you're interested in the math that Everstrike uses to calculate its Mark Price, make sure to check out this article.

In a nutshell, Everstrike calculates an impact price (average fill price for large orders in either market direction) for every second of market activity, averages the impact prices throughout the last 30 seconds, and scales the final result to be within a certain range of the Black-Scholes price of the contract.

This captures the generally accepted market price (as evidenced by order-book data), and makes it immune to manipulation.