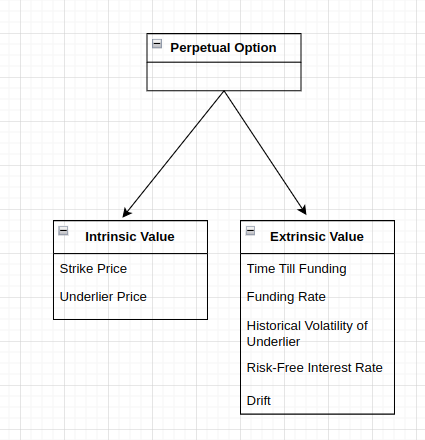
The Perpetual Option
The Perpetual Option is a funding-based derivative that can express an arbitrary number of payoff functions, including the one used by the Perpetual Future. This document provides a high-level overview of the Perpetual Option.
Funding-Based Derivatives
Funding-based derivatives are financial derivatives that include a Funding component. They originated in the late 1980’s, and are currently dominating the cryptocurrency derivatives markets.
Most funding-based derivatives are perpetual.
The Perpetual Option
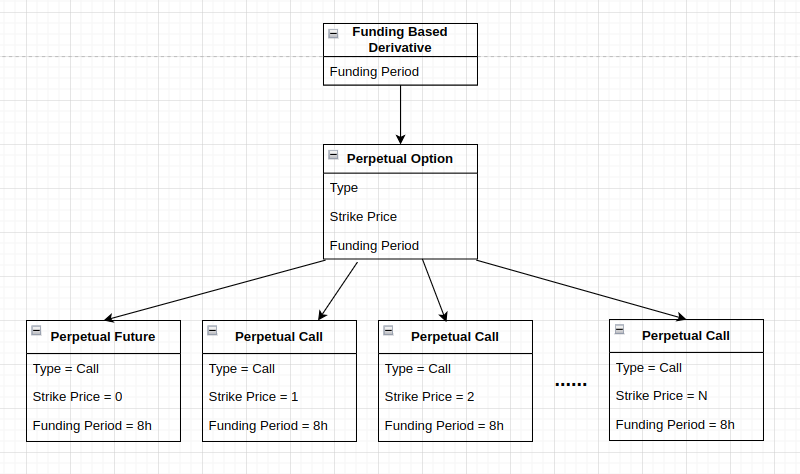
The Perpetual Option is an example of a funding-based derivative. It has three primary properties:
- Type (Call or Put)
- Strike Price
- Funding Period
By varying these properties, it is possible for the Perpetual Option to express an arbitrary number of payoff functions.
The Perpetual Future
The simplest (and most popular) instance of the Perpetual Option looks like this:
Type: Call
Strike Price: 0
Funding Period: 8 hours
This particular instance of the Perpetual Option is most commonly known as the Perpetual Future.
Additional Properties
Index Price
The Index Price represents the intrinsic value of a Perpetual Option.
Fair Price
The Fair Price represents the generally accepted market value of a Perpetual Option.
It is calculated directly from order book data.
A simplified formula for the Fair Price looks like this:
Fair Price = Best Bid + (Best Ask — Best Bid) / 2,
where Best Bid is the bid (X dollars deep in the order book), and Best Ask is the ask (X dollars deep in the order book).
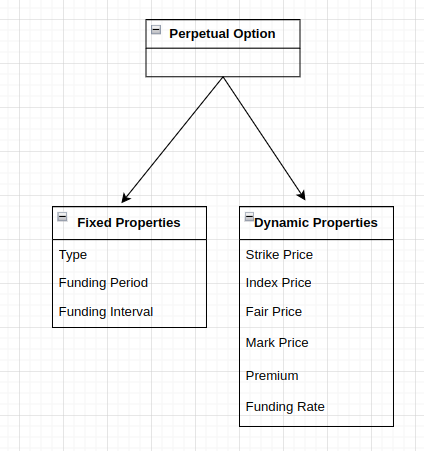
Mark Price
The Mark Price represents the generally accepted market value of a Perpetual Option, throughout the last X time periods. It is calculated directly from the Fair Price.
A simplified formula for the Mark Price looks like this:
Mark Price = EMA30(Fair Price)
where EMA30 is the 30-period exponential moving average and each period is 1 second.
Calculation of the Mark Price requires regular sampling of the Fair Price. In the above example, the Fair Price would need to be sampled once every second.
Premium
The premium of a Perpetual Option is defined as the difference between the market value of the option throughout the last X time periods (Mark Price) and the intrinsic value of the option (Index Price).
Premium = Mark Price — Index Price
Funding Rate
The Funding Rate of a Perpetual Option is determined by the value of its premium throughout the last X time periods. A simplified formula for the Funding Rate could look like this:
Funding Rate = EMA60(Premium/Index Price),
where EMA60 is the 60-period exponential moving average, and each period is 1 minute.
Calculation of the Funding Rate requires periodic sampling of the premium. In the above example, the premium would need to be sampled once every minute.
Funding Rate Constraints
In practice, the Funding Rate is often subject to constraints:
Funding Rate = Min(0.015, Funding Rate)
The Funding Rate is typically also rounded to a multiple of 0.0001.
Funding
A Perpetual Option is subject to Funding. Funding is a periodic exchange of money between longs and shorts. The amount exchanged (Funding Payment) is determined by the Funding Rate:
Funding Payment = Funding Rate * Position Size
If the Funding Rate is positive, longs pay shorts.
Otherwise, shorts pay longs.
Funding takes place at the end of each Funding Interval.
The purpose of Funding is to minimize the premium of the Perpetual Option. It does so by incentivizing being short (when the premium is positive), and by incentivizing being long (when the premium is negative).
Pricing
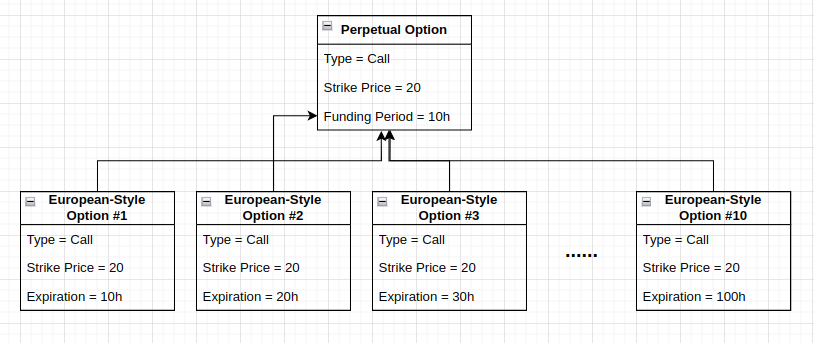
To price a Perpetual Option, split the option into N European-style Options.
Each European-style Option should have the same Strike Price and Type as the original Perpetual Option.
Assign a unique Weight and Expiration to each European-style Option, based on the following pattern:
European-style Option #1: Expiration = 1 * Funding Period, Weight = 0.5¹
European-style Option #2: Expiration = 2* Funding Period, Weight = 0.5²
…
European-style Option #N: Expiration = N* Funding Period, Weight = 0.5n
You can choose N=10.
Next, price each European-style Option using your preferred pricing model (Black & Scholes, Binomial, other). You will now have N different prices.
Finally, calculate the weighted sum of your N prices (using the weights from above). This will be the price of the original Perpetual Option.
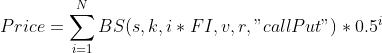
Example
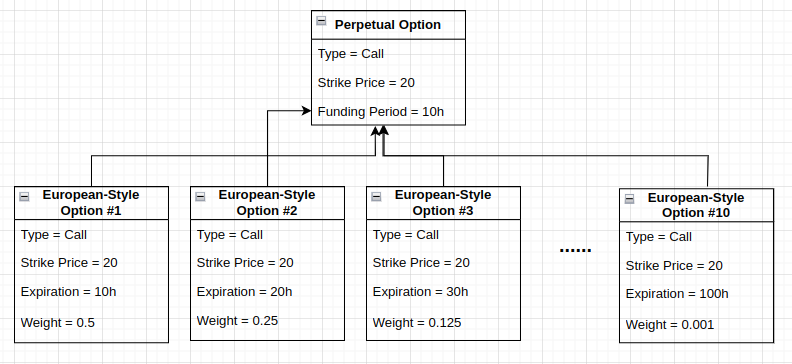
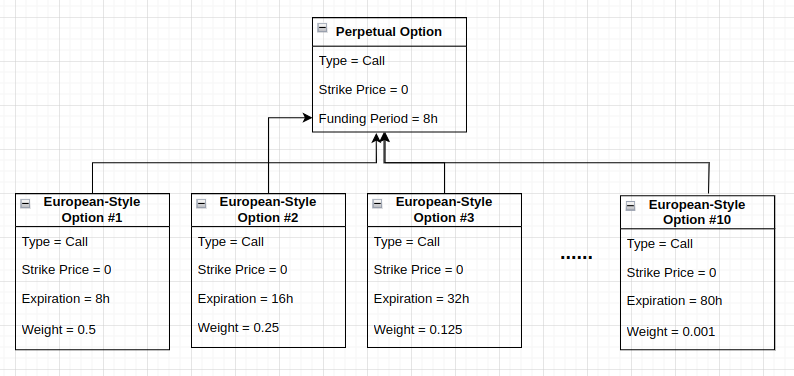
Consider the Perpetual Call Option with Strike Price 0 and Funding Period 8h (Perpetual Future).
We can price this option using the method above.
First, divide the option into 10 European-style Options:
European-style Option #1: Type = Call, Strike Price = 0, Expiration = 8h, Weight = 0.5¹
European-style Option #2: Type = Call, Strike Price = 0, Expiration = 16h, Weight = 0.5²
…
European-style Option #10: Type = Call, Strike Price = 0, Expiration = 80h, Weight = 0.5¹⁰
Next, calculate the price of each European-style Option (using Black & Scholes).
Finally, sum the values together, applying the weights from above.
You should arrive at a value that closely resembles the spot price of the Perpetual Option’s underlying asset.
Greeks
To calculate the greeks (delta, gamma, theta, vega) of a Perpetual Option, apply the same method as above, but solve for delta/gamma/theta/vega instead of price.
Approximate Pricing
Sometimes, it may be desirable to quickly calculate the approximate price of a Perpetual Option.
To do so, calculate the price of an equivalent European-style Option with:
Expiration = Funding Period * 2.
This will give you a ballpark estimate of the Perpetual Option’s value.
You can also use this heuristic to derive the approximate greeks of a Perpetual Option.
Funding Period
As we saw above, the Funding Period of a Perpetual Option is a proxy for its expiration.
This proxy is used when pricing the option, and for calculating the greeks of the option.
A Perpetual Option with a Funding Period of 10 hours is (very roughly) priced like a 0DTE European-style Option, while a Perpetual Option with a Funding Period of 1 week is (very roughly) priced like a 14DTE European-style Option.
Strike Price
A Perpetual Option can have either a Fixed Strike Price, or a Floating Strike Price.
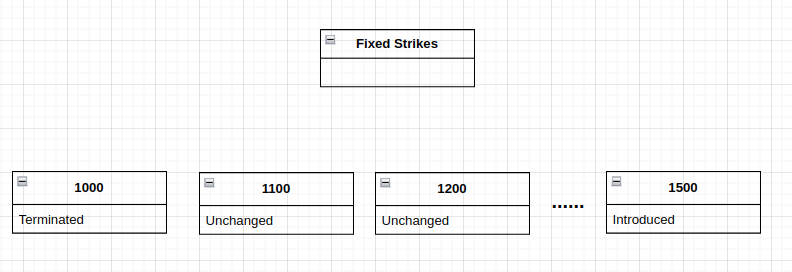
A Fixed Strike Price Perpetual Option is easy to price, but not very flexible. Fixed Strike Perpetual Options Markets suffer from significant liquidity fragmentation, and require a Strike Introduction Policy and Strike Termination Policy to be successful.
A Floating Strike Price Perpetual Option is the opposite. It is hard to price, but very flexible. Floating Strike Perpetual Options Markets require only a few contracts to be successful. No Strike Introduction Policy or Strike Termination Policy is required.
From a liquidity perspective, the Floating Strike Perpetual Option is superior.
From a pricing perspective, the Fixed Strike Perpetual Option is superior.
In order to be successful, Fixed Strike Perpetual Options Markets typically require a Strike Introduction Policy and a Strike Termination Policy. At the end of each time period, a number of new Strike Prices are introduced, and a number of existing Strike Prices are terminated. Having such a policy violates the perpetual nature of the Perpetual Option, and is why designers of Perpetual Options Markets typically prefer Floating Strike Prices.
The Future of the Perpetual Option
The Perpetual Option has already seen significant adoption within the cryptocurrency niche. However, this adoption has been limited to a specific instance of the Perpetual Option (the Perpetual Future).
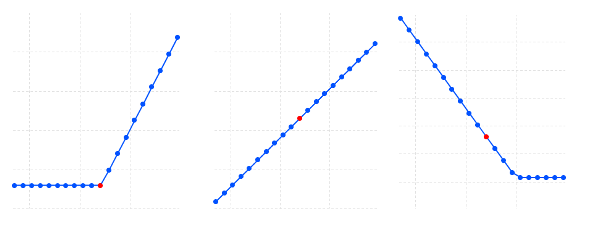
In hindsight, it was obvious that the Perpetual Future would be adopted first. After all, it is the simplest version of the Perpetual Option. The price of the Perpetual Future closely resembles the spot price of its underlying asset, making it easy for traders to understand it.
With the Perpetual Future taking up more than 93% of cryptocurrency derivatives volume, we believe that it is now time to explore other instances of the Perpetual Option. Particularly, we see a need for instances of the Perpetual Option that can offer positive convexity. The linear P/L curve of the Perpetual Future is easy to understand, but not powerful enough to satisfy the needs of the next generation of cryptocurrency traders.
Everstrike
Everstrike offers Floating Strike Perpetual Options for BTC and ETH.
The options have a Funding Period of 10 hours.
Everstrike chose this particular Funding Period to achieve a greeks profile similar to that of 0DTE European-style Options. 0DTE European-style Options dominate the global options markets, making up more than 40% of the overall trading volume. Having access to perpetual options is particularly important for traders of 0DTE options, as the costs associated with rolling on a daily basis can be significant.
The Perpetual Options on Everstrike have Floating Strike Prices (pinned around the 100-hour EMA of the underlier). No Strike Introduction Policy or Strike Termination Policy is required. By combining a long EMA (100 hours) with a short Funding Period (10 hours), the options remain relatively easy to price.
